Antwort Wann ist etwas logisch äquivalent? Weitere Antworten – Wie erkennt man, ob es logisch äquivalent ist
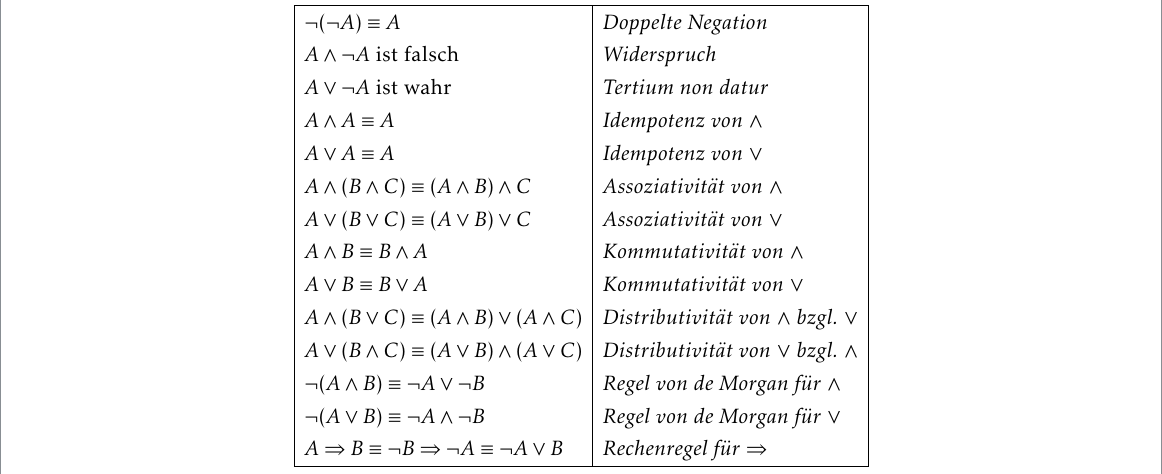
Zwei Ausdrücke sind logisch äquivalent , sofern sie für alle möglichen Kombinationen von Wahrheitswerten für alle in den beiden Ausdrücken vorkommenden Variablen denselben Wahrheitswert haben . In diesem Fall schreiben wir X≡Y und sagen, dass X und Y logisch äquivalent sind.Die Aussage A , B ist genau dann wahr, wenn A und B den gleichen Wahrheitsgehalt haben, also beide falsch oder beide wahr sind. Wir sagen dann, dass die Aussagen A und B äquivalent sind. In vielen mathematischen Sätzen ist die Äquivalenz zweier Aussagen durch die Formulierung „ge- nau dann, wenn“ gekennzeichnet.Vereinfacht ausgedrückt ist „Nicht (P oder Q)“ logisch äquivalent zu „Nicht P und Nicht Q“ . Darüber hinaus gilt dieses Prinzip auch für bedingte Anweisungen. Eine bedingte Aussage „Wenn P, dann Q“ hat die logische Äquivalenz von „Nicht P oder Q“.

Welche zwei Aussagen sind logisch äquivalent : Logische Äquivalenz liegt vor, wenn zwei Aussagen den gleichen Wahrheitswert haben . Das bedeutet, dass eine Aussage in ihrem eigenen Kontext wahr sein kann und die zweite Aussage auch in ihrem eigenen Kontext wahr sein kann, nur müssen beide die gleiche Bedeutung haben.
Woher wissen Sie, ob zwei Aussagen logisch äquivalent sind
Zwei Aussageformen sind genau dann logisch äquivalent, wenn ihre resultierenden Wahrheitstabellen für jede Variation von Aussagevariablen identisch sind . pq und qp haben die gleichen Wahrheitswerte, sind also logisch äquivalent.
Welche Sätze sind logisch äquivalent : Die Sätze sind gleich oder logisch äquivalent , wenn sie immer den gleichen Wahrheitswert haben . Das heißt, p und q sind logisch äquivalent, wenn p immer dann wahr ist, wenn q wahr ist, und umgekehrt, und wenn p immer dann falsch ist, wenn q falsch ist, und umgekehrt.
P → Q ist logisch äquivalent zu ¬ P ∨ Q .

Nehmen Sie zum Beispiel die Aussage „Wenn eine gerade Zahl ist, dann ist eine ganze Zahl.“ Eine äquivalente Aussage ist: „ Wenn es keine ganze Zahl ist, dann ist es nicht gerade .“ Die ursprüngliche Aussage hatte die Form „Wenn A, dann B“ und die zweite die Form „Wenn nicht B, dann nicht A.“ (Hier ist A die Aussage „ist gerade“, also ist „nicht A“ die Aussage „ist nicht gerade“ …
Was meinst du mit logischer Äquivalenz
Zwei logische Aussagen sind logisch äquivalent , wenn sie immer den gleichen Wahrheitswert ergeben . Folglich ist p≡q dasselbe, als würde man sagen, dass p⇔q eine Tautologie ist. Denken Sie neben dem Verteilungsgesetz und dem De-Morgan-Gesetz auch an diese beiden Äquivalenzen. Sie sind sehr hilfreich bei der Bewältigung von Implikationen.Zwei logische Aussagen sind logisch äquivalent , wenn sie immer den gleichen Wahrheitswert ergeben . Folglich ist p≡q dasselbe, als würde man sagen, dass p⇔q eine Tautologie ist. Denken Sie neben dem Verteilungsgesetz und dem De-Morgan-Gesetz auch an diese beiden Äquivalenzen. Sie sind sehr hilfreich bei der Bewältigung von Implikationen.Zwei Sätze sind genau dann logisch äquivalent, wenn sie durch denselben Satz von Wahrheitszuweisungen erfüllt werden . Erinnern Sie sich nun an die Semantik von Sätzen mit dem Bikonditionaloperator. Ein Bikonditional ist genau dann wahr, wenn die Wahrheitswerte der Bedingungssätze gleich sind.
Da eine Umkehrung das Kontrapositiv der Umkehrung ist, sind Umkehrung und Umkehrung logisch äquivalent zueinander .
Wie zeigt man eine Äquivalenz : Um zu prüfen, ob zwei Terme äquivalent zueinander sind, kannst du wie folgt vorgehen:
- Vereinfache den ersten Term, so weit es geht.
- Vereinfache den zweiten Term, so weit es geht.
- Sortiere die beiden Terme in der gleichen Reihenfolge.
- Prüfe, ob die Terme gleich sind.
Wie beweisen Sie, dass zwei Aussagen nicht logisch äquivalent sind : Um zu zeigen, dass eine Aussage nicht logisch äquivalent zu einer Aussage ist , zeigen wir, dass sie nicht die gleiche Wahrheitstabelle haben . Beispielsweise sind Aussagen P → Q, ∼ P → ∼ Q (invers) nicht logisch äquivalent, da sie nicht die gleichen Wahrheitswerte haben, wie unten gezeigt.
Sind Bedingung und Umkehrung logisch äquivalent
Eine bedingte Anweisung ist logisch nicht äquivalent zu ihrer Umkehrung . Nur wenn: p nur wenn q bedeutet „Wenn nicht q, dann nicht p“ oder äquivalent: „Wenn p, dann q.“

Beispielsweise sind die Terme "2x" und "x + x" äquivalent, da sie für jeden Wert von x den gleichen Wert aufweisen. Wenn x beispielsweise den Wert 3 hat, dann hat "2x" den Wert 6 und "x + x" den Wert 6. Daher sind beide Terme äquivalent.Äquivalenzrelation einfach erklärt
Mit einer Äquivalenzrelation kannst du Beziehungen zwischen Dingen in einer Menge darstellen. Dabei werden zwei Dinge „äquivalent“ genannt, wenn sie gleiche oder ähnliche Eigenschaften haben.
Wie zeigt man dass zwei Terme äquivalent sind : Um zu prüfen, ob zwei Terme äquivalent zueinander sind, kannst du wie folgt vorgehen:
- Vereinfache den ersten Term, so weit es geht.
- Vereinfache den zweiten Term, so weit es geht.
- Sortiere die beiden Terme in der gleichen Reihenfolge.
- Prüfe, ob die Terme gleich sind.

![csm_2405-bauerfeind-produktkategoriesseiten-bandagen-ellenbogenbandage-2560x1400_88-1_f91f66009c[1]](https://www.nakajimamegumi.com/wp-content/uploads/2024/06/csm_2405-bauerfeind-produktkategoriesseiten-bandagen-ellenbogenbandage-2560x1400_88-1_f91f66009c1-1024x521-65x65.jpg)
![Ischiasschmerzen[1]](https://www.nakajimamegumi.com/wp-content/uploads/2024/06/Ischiasschmerzen1-1024x640-65x65.jpg)
![csm_blogbeitrag_autoimmunerkrankung_d307ac8b72[1]](https://www.nakajimamegumi.com/wp-content/uploads/2024/06/csm_blogbeitrag_autoimmunerkrankung_d307ac8b721-1024x576-65x65.jpeg)