Antwort Was ist die Nullstellenform? Weitere Antworten – Wie kommt man auf die Nullstellenform

Die Nullstellenform ist eine von vier verschiedenen Möglichkeiten zur Darstellung einer quadratischen Funktion. Diese Möglichkeiten sind: Die allgemeine Form: f ( x ) = a ⋅ x 2 + b ⋅ x + c f(x)=a\cdot x^2+b\cdot x+c f(x)=a⋅x2+b⋅x+c.Eine Funktion hat zwei Nullstellen, wenn die beiden Schenkel der Parabel die x-Achse schneiden. Sie hat nur eine Nullstelle, wenn nur der Scheitelpunkt der Parabel die x-Achse berührt.Hier die Lösungsschritte zusammengefasst:
- Funktion gleich null setzen, f(x) = … =
- Konstantes Glied (also ohne x ) nach rechts bringen.
- Durch etwaigen Vorfaktor vor der Klammer dividieren.
- Wurzel ziehen (dabei Plus-Minus-Vorzeichen berücksichtigen)
- Lösungen ausrechnen und aufschreiben.

Wie berechnet man die Nullstellen einer Funktion : Der Wert einer Wurzel ist null, wenn der Radikand (der Wert unter der Wurzel) null ist. Um die Nullstelle zu berechnen, nimmst Du nur den Radikand, also den Term unterhalb der Wurzel und setzt ihn gleich 0. Die Nullstelle befindet sich also am x-Wert 2.
Was sind Nullstellen bei quadratischen Gleichungen
Im Falle der quadratischen Funktion sind die Nullstellen die Stellen, an denen der Graph der Funktion f(x) die x-Achse schneidet. Im Falle der quadratischen Funktion sind dies genau die x-Werte, an der der Graph die x-Achse schneidet. Der Wert der y-Koordinate muss also 0 sein.
Wie liest man Nullstellen ab quadratische Funktion : 0:46Empfohlener Clip · 49 SekundenNullstellen berechnen | einfach erklärt von Lehrerschmidt – YouTubeBeginn des vorgeschlagenen ClipsEnde des vorgeschlagenen Clips
Die Nullstellenform f(x) = a • (x – x1) • (x – x2) ist eine von drei Möglichkeiten zur Darstellung einer (quadratischen) Funktion, aus der man die Nullstellen ablesen kann. Weitere Möglichkeiten sind die Normalform und die Scheitelpunktform.
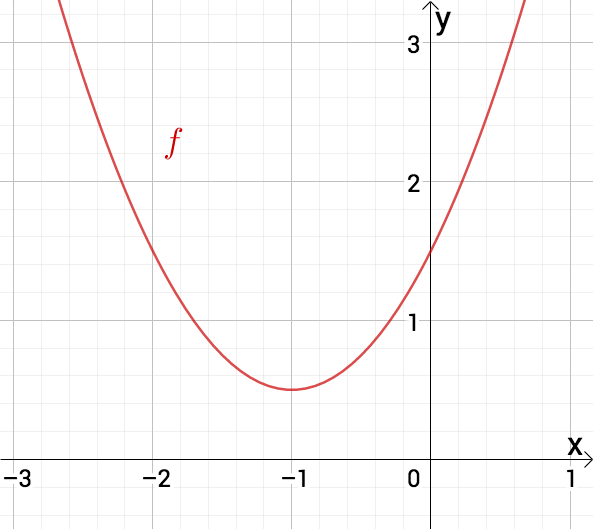
Der Scheitelpunkt ist der höchste bzw. tiefste Punkt einer Parabel. Du kannst den Scheitelpunkt aus der Scheitelpunktform f(x) = a(x-d)²+e ablesen: S (d | e).
Wie viele Nullstellen hat die Funktion
Eine quadratischen Funktion kann maximal zwei Nullstellen haben. Deren Bestimmung läuft auf das Lösen einer quadratischen Gleichung hinaus.Anzahl der Nullstellen anhand der Diskriminante bestimmen
Die Anzahl der Nullstellen einer quadratischen Funktion f entspricht der Anzahl der Lösungen der quadratischen Gleichung f(x)=0. Daher kannst du die Anzahl der Nullstellen anhand der Diskriminante der quadratischen Gleichung bestimmen. D=294>0.Eine quadratische Funktion kann keine, eine oder zwei Nullstellen haben. Wenn der Tiefpunkt über der x-Achse liegt, hat die Funktion keine Nullstelle. Berührt die Funktion die x-Achse, so liegt nur eine Nullstelle vor. Nun hast du einen Überblick über die quadratischen Funktionen bekommen.

Eine quadratischen Funktion kann maximal zwei Nullstellen haben.
Was ist eine Nullstelle quadratische Funktionen : Die Nullstellen einer quadratischen Funktion sind die Punkte, an denen die Funktion die x-Achse schneidet. Eine quadratische Funktion kann zwei, eine oder keine Nullstelle haben. Die Funktion f(x) = x2 – 2 hat zum Beispiel zwei Nullstellen.
Wie berechnet man die Nullstelle mit der PQ Formel : Wie werden Nullstellen mit der PQ Formel berechnet Um die Nullstellen einer quadratischen Funktion mit der pq-Formel zu berechnen, setze die Funktion f(x) gleich Null (f(x)=0) und forme die Gleichung in die Form x²+px+q=0 um. Lies die Koeffizienten p und q aus, setze sie in die pq-Formel ein und rechne die Formel aus.
Wie berechnet man die Nullstelle bei einer quadratischen Funktion
Du kannst die Nullstellen von quadratischen Funktionen f(x) = ax2 + bx – c immer mit der Mitternachtsformel berechnen. Dafür brauchst du nur die Zahl vor dem x2 (a), die Zahl vor dem x (b) und die Zahl ohne x (c). Hier ist a = 2 (Zahl vor dem x2), b = 4 (Zahl vor dem x) und c = -6.
Normalform: f(x)=ax2+bx+c. Scheitelpunktform: f(x)=a(x−d)2+e, dabei ist der Punkt S(d|e) der Scheitelpunkt der Parabel.Scheitelpunktform einfach erklärt
Den Scheitelpunkt kannst du daran direkt ablesen, er lautet: S(d|e). a ist ein Faktor, der die Steilheit der Parabel angibt. Beispiel: Der Scheitelpunkt der Funktion f(x) = 2 (x – 3)2 + 1 liegt bei S(3|1).
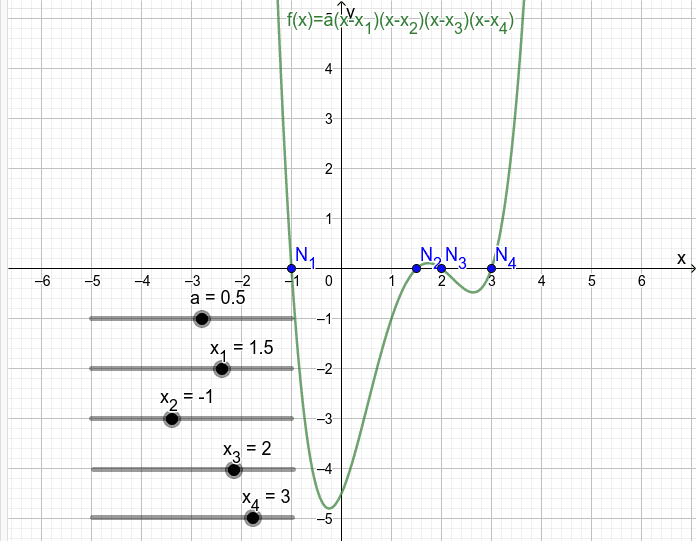
Welche Arten von Nullstellen gibt es : Die wichtigsten drei Arten von Nullstellen sind die einfache Nullstelle, die doppelte Nullstelle und die dreifache Nullstelle. Um welche Art von Nullstelle es sich handelt, kann man sowohl im Graphen als auch in einer faktorisierten Funktionsgleichung erkennen.

![csm_2405-bauerfeind-produktkategoriesseiten-bandagen-ellenbogenbandage-2560x1400_88-1_f91f66009c[1]](https://www.nakajimamegumi.com/wp-content/uploads/2024/06/csm_2405-bauerfeind-produktkategoriesseiten-bandagen-ellenbogenbandage-2560x1400_88-1_f91f66009c1-1024x521-65x65.jpg)
![Ischiasschmerzen[1]](https://www.nakajimamegumi.com/wp-content/uploads/2024/06/Ischiasschmerzen1-1024x640-65x65.jpg)
![csm_blogbeitrag_autoimmunerkrankung_d307ac8b72[1]](https://www.nakajimamegumi.com/wp-content/uploads/2024/06/csm_blogbeitrag_autoimmunerkrankung_d307ac8b721-1024x576-65x65.jpeg)